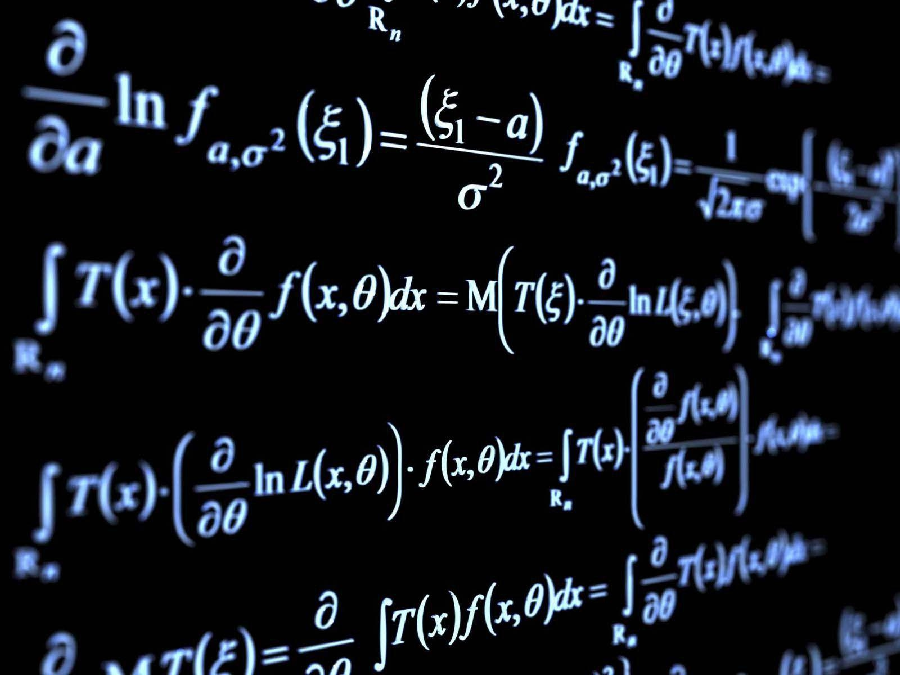In Mathematics, Euclidean Geometry (also known as “Geometry”) is the study of various flat shapes based on different theorems and axioms. In schools, we have learned different concepts of Euclidean geometry such as points, lines, angles, planes, flat figures, solid figures and so on. The applications of Euclidean geometry plays a vital role in many scientific areas such as Astronomy, Crystallography and technical areas like Architecture, Engineering, Navigation, Aerodynamics and so on. Now, let us look at the applications of Euclid’s Geometry in detail.
Architecture
The application of geometry is found extensively in architecture. Nowadays, Computer-Aided Design (CAD) and Computer-Aided Manufacturing (CAM) is based on Euclidean Geometry. The most important fundamental concept in architecture is the use of triangles. Architects generally use the triangle shape to construct the building. The congruence of triangles helps them to calculate the forces applied to the building. The triangle congruences are used to check whether the given forces are appropriately balanced so that the building will not collapse.
Astronomy
Astronomy means the science of matter and objects beyond the Earth’s atmosphere such as space, celestial bodies and so on. Astronomers use Maths all the time. Initially, they use Maths to count the objects and entities in the sky during the daytime or at night. Later, they use Geometry in astronomy to calculate the direction, speed, velocity, momentum, the relativity of many celestial bodies.
Navigation
The Euclid System was incredibly powerful and developed a set of tools to navigate on the surface of the Earth, assuming that the Earth was flat. The two key concepts in Euclidean geometry are angle and length. To navigate on land or on the ship, two things we need to know are which direction we are heading and how far we have travelled. Later on, many scientists proved that Earth is a sphere. They proved that Earth resembles to be flat from our vantage point, but actually, it is spherical. It leads to the development of the spherical geometry called the non-Euclidean geometry.
Hang Gliders
In the design of hang glider shapes, the designers use the orthocenter of the glide to make sure the cords descending from the glide to the rider are an exact length, which connects at the point of concurrency. The orthocenter of the glide will be on the outside of the triangle, as the glide itself is an obtuse triangle.
Engineering
Geometry is almost used in all the branches of engineering. In civil engineering, geometry is widely used to construct the building, which helps them to calculate the spacing of their beams for the proper strength of the building. In computer science, the application of computational geometry includes Geographical Information System (GIS), robotics, Computer-Aided Engineering and so on. Computational geometry is a branch that involves the mathematical design, analysis, and the implementation of the efficient algorithm to solve the geometric inputs and outputs. From robotics to the manufacturing of cars, engineers use geometry to visualize and draw out the design on blueprints with the help of many geometrical tools such as protractor and compass.