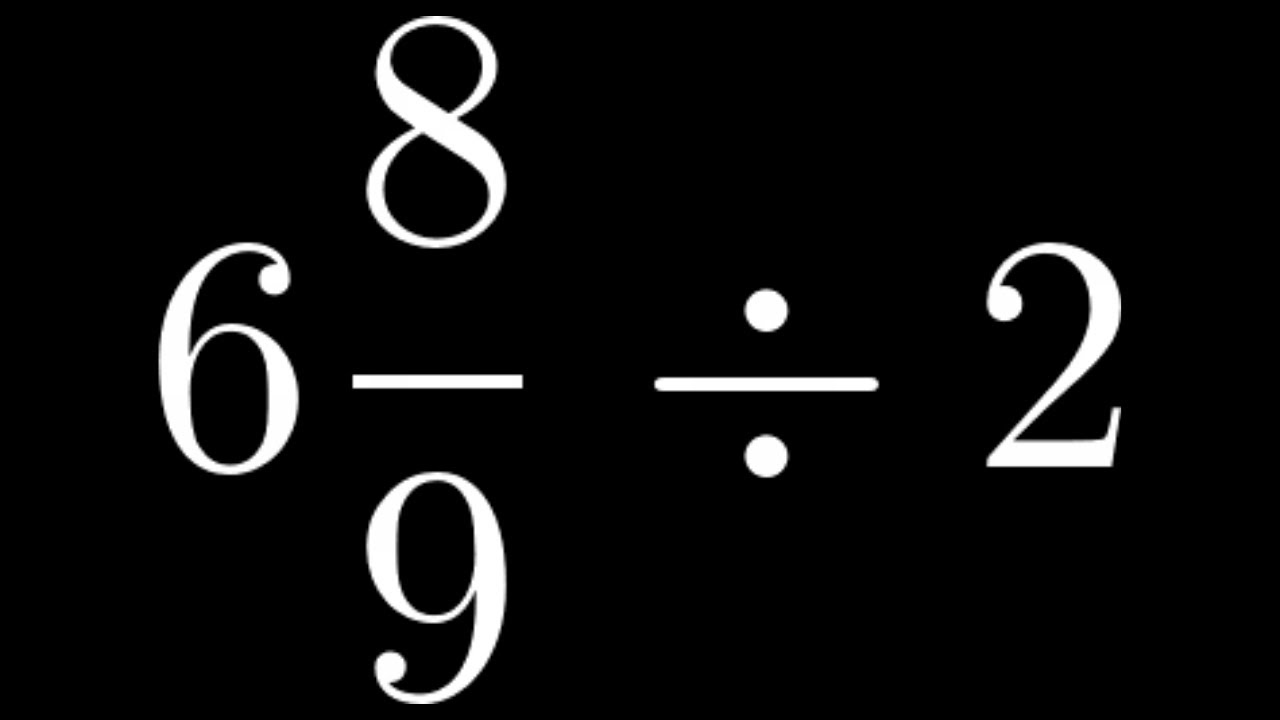Introduction:
Division is a fundamental arithmetic operation that involves sharing or grouping a quantity into equal parts. Whether dealing with whole numbers or decimal numbers, the division process remains a crucial skill in mathematics. In this article, we will explore the step-by-step procedures for both whole number and decimal number division, providing clarity on these essential mathematical concepts.
Whole Number Division:
1. **Setting Up the Division:**
The first step in whole number division is to set up the division problem. Place the dividend (the number to be divided) inside the long division bracket and the divisor (the number by which the division is to be performed) outside the bracket.
2. **Dividing the Digits:**
Begin dividing the digits of the dividend by the divisor. In our example, 24 divided by 3 equals 8. Write the quotient (8) above the division bracket.
3. **Multiplying and Subtracting:**
Multiply the divisor by the quotient and subtract the result from the dividend. Repeat this process until there is no remainder.
4. **Checking for Remainder:**
Ensure that there is no remainder left. In this case, the division is exact, and the result is the quotient.
Decimal Number Division:
1. **Decimal Placement:**
When dealing with decimal numbers, align the decimal points in the dividend and divisor.
2. **Removing Decimal Point:**
Eliminate the decimal point in the divisor by multiplying both the divisor and dividend by a power of 10 to make the divisor a whole number.
3. **Divide as Whole Numbers:**
Apply the whole number division process as described earlier.
4. **Reintroduce the Decimal Point:**
Place the decimal point in the quotient directly above its position in the dividend.
Mastering the division process is essential for solving mathematical problems efficiently. Whether working with whole numbers or decimal numbers, following these step-by-step procedures will lead to accurate results. Regular practice and understanding of these concepts will enhance mathematical proficiency and contribute to overall mathematical competence.